Our dedication to Racial Equality and Social Justice (RESJ) spans decades. Learn more about our RESJ Initiative
Math Matters - The Golden Ratio
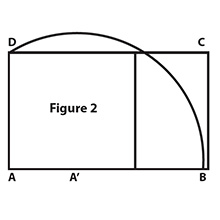
The Golden Ratio (a.k.a. Golden Mean) was discovered by the ancient Greeks and was considered a thing of great beauty. It was a ratio revered through the ages. A rectangle whose length-to-width ratio is the Golden Mean is a Golden Rectangle. [Sidebar 1: put a “co” in front of rectangle and you get co-rectangle because it is made from four correct a.k.a. right angles.] I’ve read that buildings constructed in the early nineteenth century had their window dimensions in this ratio because it made these buildings more aesthetically pleasing to the eyes – possibly a big deal to city newcomers.
But if it was the Greek mathematicians who created the Golden Rectangle, it was Western bankers who created the Gold Card. What we want to do is to see if there is any connection. This will require both algebraic and geometric manipulation – in the right proportions of course.
First the algebra: A line-segment [A, C] divided by point B so that AB/BC = AC/AB is divided into Golden Ratio proportions. By letting x = AB and making the distance from B to C = 1, we have x/1 = (x + 1)/ x. See Figure 1 which is helpful. Cross-multiplying yields the quadratic x2 – x – 1 = 0. Applying the quadratic formula gives us: x = (1 + 5)/2. [Sidebar 2: the other solution to the quadratic equation, (1 – 5)/2, interestingly, is the additive-inverse of its multiplicative-inverse.] This is an irrational...
Continued on September 2016 Newsletter

